Le leggi del moto armonico
Le ultime considerazioni ci portano ad affermare che il periodo del moto armonico è uguale a quello del moto circolare associato.
Poiché nel moto armonico di una molla abbiamo già stabilito
che ![]() , deduciamo che la pulsazione angolare del moto associato è
data da
, deduciamo che la pulsazione angolare del moto associato è
data da ![]() , e quindi il periodo è dato
da
, e quindi il periodo è dato
da ![]() o, in alternativa,
o, in alternativa,
![]()
che conferma quanto possiamo ritrovare con le esperienze descritte in un'altra parte di questo sito, cioè
Nel moto armonico di un corpo appeso ad una molla il quadrato del periodo di ogni oscillazione è direttamente proporzionale alla massa del corpo ed inversamente proporzionale alla costante elastica della molla.
| Per ricavare la legge oraria del moto dobbiamo ricorrere alle funzioni goniometriche. |
|
| Infatti è evidente dalla figura che la legge è esprimibile
facendo uso della funzione seno (o, ugualmente, della funzione coseno),
attraverso la relazione |
|
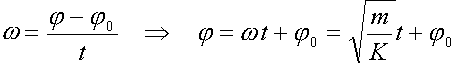
L’angolo ![]() prende il nome di fase
dell’oscillatore, mentre l’angolo
prende il nome di fase
dell’oscillatore, mentre l’angolo ![]() , che dipende esclusivamente dall’istante in cui cominciamo a
misurare il tempo t, è detto fase iniziale. Con tali
considerazioni, otteniamo la legge oraria del moto armonico di un corpo appeso
ad una molla:
, che dipende esclusivamente dall’istante in cui cominciamo a
misurare il tempo t, è detto fase iniziale. Con tali
considerazioni, otteniamo la legge oraria del moto armonico di un corpo appeso
ad una molla:
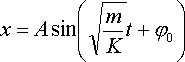
Questa formula, che esprime la posizione del corpo in moto in funzione del tempo, rappresenta la soluzione dell’equazione differenziale introdotta in precedenza.