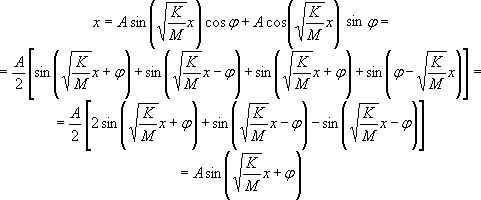L'equazione differenziale del moto armonico

E` opportuno ricordare che  e quindi l’equazione del moto armonico diviene

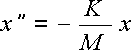
Tale equazione è detta differenziale. Per la precisione, un’equazione differenziale è un equazione in cui l’incognita è costituita da una funzione ed in cui compaiono operatori differenziali, in particolare l’operazione di derivata. L’integrale indefinito, ossia la ricerca delle primitive di una funzione, è il primo esempio di equazione differenziale.

Si dice ordine dell’equazione differenziale il massimo ordine di derivazione presente. Come già noto per l’integrale indefinito le soluzioni di un’equazione differenziale non sono uniche, ma presentano delle costanti arbitrarie in numero pari all’ordine dell’equazione. L’insieme di tutte le soluzioni di un’equazione differenziale si dice integrale generale dell’equazione.

Un’equazione è detta parimenti omogenea se non compare esplicitamente la variabile (in questo caso il tempo t) di derivazione, mentre si dice lineare se la funzione incognita e le sue derivate sono presenti al primo grado. Un’equazione come quella del moto armonico è quindi un’equazione lineare omogenea, a coefficienti costanti, del second’ordine.

La linearità dell’operazione di derivata fa si che se disponiamo di una soluzione di un’equazione differenziale lineare, anche tutti i suoi multipli sono soluzioni. Prendiamo per esempio l’equazione in oggetto se x è una soluzione e B un numero reale qualsiasi, otteniamo

Quindi anche Bx è soluzione dell’equazione. Analogamente se le funzioni f e g sono soluzioni anche f+g lo è. (La verifica è del tutto analoga a quella precedente). Per ottenere quindi l’integrale generale dell’equazione in oggetto è sufficiente trovare due soluzioni particolari f e g, linearmente indipendenti (cioè che non siano una multipla dell’altra). L’integrale generale sarà costituito da .

Due soluzioni particolari dell’equazione del moto armonico sono date da

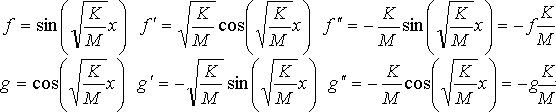
l’integrale generale è quindi

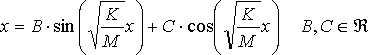
Poniamo ora , l’integrale generale, facendo uso delle formule di Werner, diviene