La definizione di moto armonico

La legge di Hooke ci ha portato alla relazione

dove il vettore x  indica lo spostamento dalla posizione di equilibrio. Da tale legge, ricordando il secondo principio della dinamica, ricaviamo l’equazione del moto di un punto materiale di massa m, libero di muoversi su un piano orizzontale privo di attrito, soggetto solo alla forza di richiamo  sotto l’azione di una molla, inizialmente perturbata dal suo stato di equilibrio:

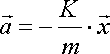
Un punto materiale, di massa m, può essere agganciato a un estremo di una molla di costante k, disposta verticalmente, il cui secondo estremo sia vincolato; a causa del peso P la molla si allunga. Esiste una configurazione di equilibrio, a cui è associata la relazione P+ F= 0 ossia P = k (x₀ - x_m) ove x₀ è la posizione di equilibrio senza il peso, x_m quella con il peso. Se lo stesso punto materiale oscilla verticalmente, l’equazione della dinamica è P - k (x₀ - x) = ma, ma tenuto conto della precedente equazione si ottiene ma = - k (x₀ - x) quindi, indicando con il vettore x lo spostamento dalla nuova posizione di equilibrio riotteniamo la stessa equazione di cui sopra.

Il moto in questione è quindi caratterizzato dall’avere accelerazione direttamente proporzionale, ma in verso opposto, allo spostamento dalla posizione di equilibrio dell’oggetto in questione. Tale spostamento x prenderà il nome di elongazione.

Un moto siffatto sarà detto armonico:

Definizione: Si dice moto armonico un moto oscillatorio, periodico, rettilineo, in cui l’accelerazione è direttamente proporzionale all’elongazione, ma diretta in verso opposto.

Il moto del corpo appeso ad una molla è, naturalmente, armonico solo in assenza di attrito, o se l'attrito è trascurabile. Altrimenti le forze dissipative dell'attrito freneranno il corpo, riducendone l'ampiezza delle oscillazioni fino a fermarlo. Un tale moto prende il nome di oscillatore armonico smorzato.

L’equazione che regola il moto armonico è quindi

Risulta evidente, dal verso dell’accelerazione, il fatto che, quando il corpo si allontana dal centro dell’oscillazione, l’accelerazione si oppone al moto e il modulo della velocità, conseguentemente, diminuisce fino ad annullarsi alle estremità. Al contrario, mentre il corpo si avvicina al centro, l’accelerazione fa aumentare il modulo della velocità, che diviene massimo proprio nel centro delle oscillazioni.

Per risolvere direttamente l’equazione riportata qui sopra, occorrerebbe far uso di abilità matematiche complesse, trattandosi di un’equazione di un particolare tipo, detta differenziale.

Possiamo, in ogni modo, ottenerne la soluzione, e la legge del moto, utilizzando un modello di moto periodico ben noto agli studenti.