Un moto teorico come modello per il moto armonico

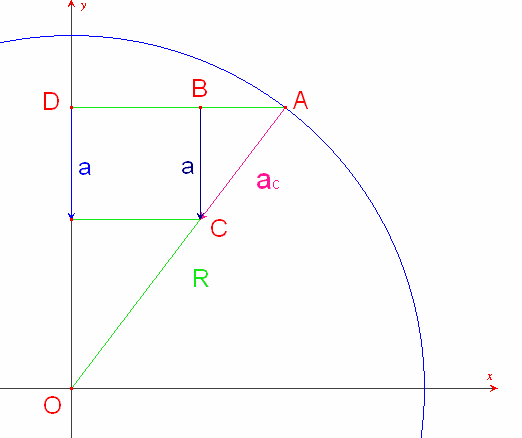
Osserviamo la seguente figura, in cui sono è messa in evidenza l’accelerazione centripeta a_c del moto circolare uniforme e la sua proiezione a sul diametro.

E` chiaro che i triangoli ABC e ADO sono simili, da cui possiamo dedurre la proporzione:

(si poteva dedurre la stessa proporzione direttamente anche con il teorema di Talete). Sostituendo alla lunghezza dei segmenti, le intensità dei vettori corrispondenti otteniamo:

da cui 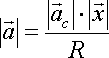  e, ricordando che nel moto circolare , dove  è la velocità angolare otteniamo 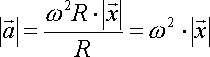. Ricordando che il vettore accelerazione, nel nostro moto, è sempre opposta allo spostamento x otteniamo la relazione vettoriale

identica a quella del moto armonico, dove si è posto la costante

Abbiamo dedotto quindi che il moto ottenuto proiettando su un diametro un punto che si muove di moto circolare uniforme è sempre un moto armonico. Possiamo ora applicare il nostro modello ad ogni moto armonico, cioè, tutte le volte che dobbiamo studiare un moto armonico, possiamo considerarlo come la proiezione di un moto circolare? La risposta è chiaramente positiva. Se noi abbiamo a che fare con un moto armonico, cioè con un moto regolato dall’equazione

potremo associare a tale moto un moto circolare, che abbia come diametro la lunghezza totale della traiettoria del moto armonico, e come  velocità angolare . Tale grandezza sarà detta pulsazione angolare del moto armonico. Si badi bene che non corrisponde alla velocità angolare di alcun moto fisicamente presente nella realtà , in quanto il moto circolare che associamo al moto armonico è puramente teorico.

Possiamo concludere quindi affermando che

Un moto armonico coincide sempre con la proiezione di un moto circolare uniforme di velocità angolare .