Relazione tra periodo e costante elastica

Vogliamo ora stabilire la relazione tra il periodo di oscillazione di un oscillatore armonico e la costante elastica della molla  che lo costituisce.

Per far ciò eseguiamo la seguente procedura sperimentale

Vengono utilizzate tutte le molle di cui è stata determinata la costante elastica, e un'unica massa che possa essere tollerata da tutte senza danni, e nello stesso tempo possa deformarle in modo da ottenere misure di periodo accettabili.

La massa prescelta è un cilindro di alluminio (si tratta in realtà di due cilindri uno cavo e uno pieno, utilizzati per lo studio della spinta di Archimede), munito di gancio. La sua massa è di 232 g.

L'obiettivo è determinare il periodo di oscillazione del sistema costituito da ciascuna molla e dalla massa nota.

Montaggio dell'apparato ed esecuzione delle misure

  1. Ad un sostegno Bunsen munito di asta trasversale viene fissato il sensore di forza della Vernier, collegato al LabPro e quindi al computer, su cui è attivo il programma Logger Pro, predisposto per una raccolta dati in tempo reale della durata corrispondente ad una dozzina di oscillazioni complete. Si suggerisce di selezionare la massima frequenza delle misure accettata dal programma;
  2. Al sensore viene appesa la molla scelta, e a quest'ultima la massa;
  3. Si azzera il sensore sul valore di peso della massa e della molla in equilibrio;
  4. Si sposta il peso dalla posizione di equilibrio, verso il basso, e lo si lascia andare, cercando di evitare - per quanto possibile - impulsi trasversali che in breve tempo si tradurrebbero in oscillazioni pendolari
  5. Si fa partire la raccolta dati sul Logger Pro
  6. Si salva il file dati con un nome riconoscibile, e lo si esporta in formato .txt

Analisi dei dati

Logger Pro fornisce due serie di misure, quella dei tempi e quella delle forze: in grafico apparirà una sinusoide, che supporremo priva di altre armoniche (non è proprio così ...): si tratta di determinarne il periodo, con la relativa incertezza. Abbiamo a disposizione diversi metodi, ciascuno con i suoi svantaggi:

  1. Misurare gli intervalli temporali tra un picco e il consecutivo con l'aiuto del programma (Analyze/Examine), prendere nota delle misure, e calcolarne media e sigma, da assumere come indicatore di incertezza.
  2. Far eseguire il "curve fitting" al programma (Analyze/Linear Curve Fit ...), scegliendo una curva del tipo A Sin[Bx + C] + D, ottenendo i valori dei quattro parametri A, B, C, D, dei quali ci interessa B, che corrisponde ad w. Da w è facile ricavare il periodo (T=2pw), solo che non abbiamo una procedura semplice per determinare l'incertezza;
  3. Importare il file in formato .txt in Excel, quindi (vedi file Periodi) - mediante una macro - localizzare i valori massimi della forza e i tempi corrispondenti, e calcolare gli intervalli tra questi ultimi. Media e sigma di tali intervalli forniranno il periodo e la sua incertezze (si esamini la macro nel file Esempio).

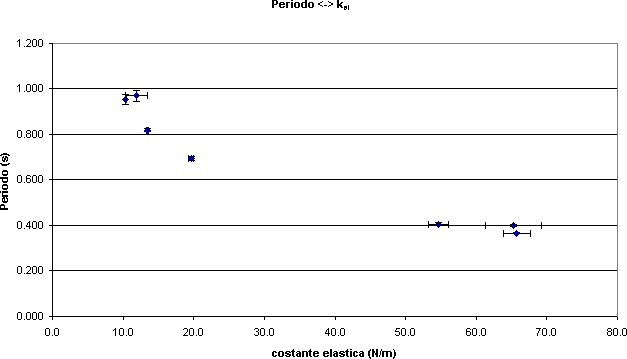
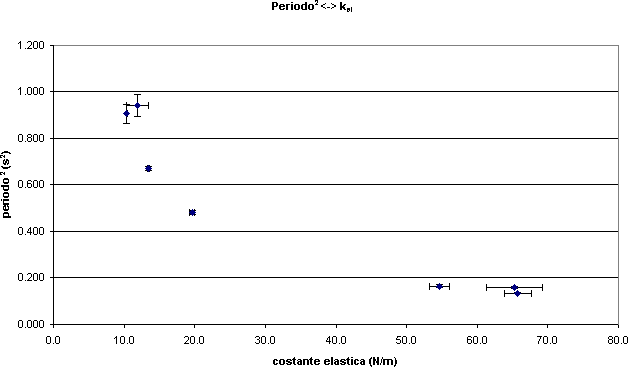
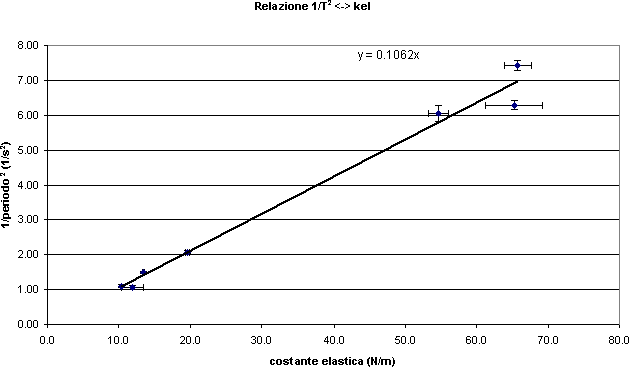
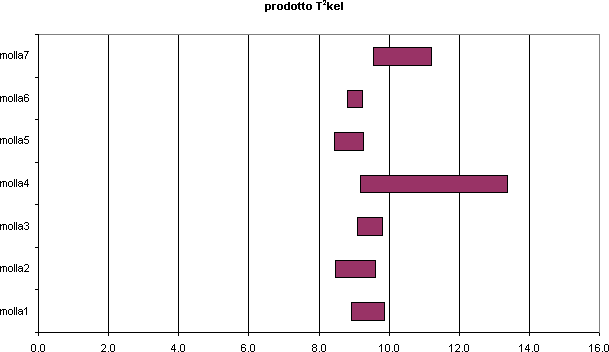
La nostra serie di misure ha portato ai seguenti risultati (vedi file Periodo_k)

 

kel

sn-1(kel)

e%(kel)

T

sn-1(T)

e%(T)

T2

sn-1(T2)

e%(T2)

1/T2

sn-1(1/T2)

e%(1/T2)

kT2

kT2 min

kT2 max

diff.

 

N/m

N/m

 

s

s

 

s2

s2

 

 

s-2

 

Ns2/m

Ns2/m

Ns2/m

Ns2/m

molla1

10.4

0.0

0.4%

0.952

0.021

2.2%

0.907

0.041

4.5%

1.10

0.05

4.5%

9.4

8.9

9.9

0.9

molla2

54.7

1.4

2.5%

0.406

0.008

1.9%

0.165

0.006

3.8%

6.06

0.23

3.8%

9.0

8.5

9.6

1.1

molla3

19.6

0.3

1.6%

0.694

0.008

1.1%

0.482

0.010

2.2%

2.08

0.04

2.2%

9.5

9.1

9.8

0.7

molla4

11.9

1.6

13.5%

0.970

0.025

2.6%

0.941

0.049

5.2%

1.06

0.05

5.2%

11.2

9.2

13.4

4.2

molla5

65.7

1.9

2.9%

0.367

0.003

0.9%

0.135

0.002

1.8%

7.42

0.13

1.8%

8.9

8.4

9.3

0.8

molla6

13.5

0.1

0.7%

0.819

0.006

0.8%

0.671

0.010

1.5%

1.49

0.02

1.5%

9.0

8.8

9.2

0.4

molla7

65.3

4.0

6.1%

0.399

0.004

1.0%

0.159

0.003

1.9%

6.29

0.12

1.9%

10.4

9.5

11.2

1.7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

media

9.6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sigma

0.9

 

 

 

Legenda:

kel

costante elastica

1/T2

reciproco periodo al quadrato

sn-1(kel)

sigma costante elastica

sn-1(1/T2)

sigma reciproco periodo al quadrato

e%(kel)

incertezza percentuale sulla costante elastica

e%(1/T2)

incertezza percentuale reciproco periodo al quadrato

T

periodo

kT2

costante el. per periodo al quadrato

sn-1(T)

sigma periodo

kT2 min

minimo prodotto k*T2

e%(T)

incertezza percentuale periodo

kT2 max

massimo prodotto k*T2

T2

periodo al quadrato

diff.

differenza

sn-1(T2)

sigma periodo al quadrato

 

 

e%(T2)

incertezza percentuale periodo al quadrato

 

 

La tabella ha lo scopo di verificare l'esistenza di una proporzionalità inversa tra costante elastica e quadrato del periodo (ovviamente a parità di massa): infatti il prodotto kT2  ha un’oscillazione del dieci percento rispetto al valore medio.  

I seguenti grafici illustrano il percorso che porta alle conclusioni di cui sopra.



 


 


L’ultimo grafico visualizza in modo efficace la proprietà individuata