Relazione tra periodo e massa

Passiamo ora a studiare la relazione tra il periodo di oscillazione di un oscillatore armonico e la massa appesa alla molla che lo costituisce.

Per far ciņ eseguiamo la seguente procedura sperimentale

Viene scelta - tra quelle di cui è stata determinata la costante elastica - una molla che abbia una buona escursione di carico, che permetta misure con masse ragionevolmente diverse. Abbiamo utilizzato la molla identificata con il n. 1

La costante elastica, misurata con la procedura descritta, è (10.37 ± 0.16) N/m, e la molla è stata caricata - senza danni apparenti - fino a 185 g.

L'obiettivo è determinare il periodo di oscillazione del sistema costituito da questa molla e da una massa nota, e di ripetere l'esperienza con un certo numero di masse diverse.

Montaggio dell'apparato ed esecuzione delle misure

  1. Ad un sostegno Bunsen munito di asta trasversale viene fissato il sensore di forza della Vernier, collegato al LabPro e quindi al computer, su cui è attivo il programma Logger Pro, predisposto per una raccolta dati in tempo reale della durata corrispondente ad una dozzina di oscillazioni complete. Si suggerisce di selezionare la massima frequenza delle misure accettata dal programma;
  2. Al sensore viene appesa la molla, e a quest'ultima la massa scelta;
  3. Si azzera il sensore sul valore di peso della massa e della molla in equilibrio;
  4. Si sposta il peso dalla posizione di equilibrio, verso il basso, e lo si lascia andare, cercando di evitare - per quanto possibile - impulsi trasversali che in breve tempo si tradurrebbero in oscillazioni pendolari
  5. Si fa partire la raccolta dati sul Logger Pro
  6. Si salva il file dati con un nome riconoscibile, e lo si esporta in formato .txt

Analisi dei dati

Logger Pro fornisce due serie di misure, quella dei tempi e quella delle forze: in grafico apparirà una sinusoide, che supporremo priva di altre armoniche (non è proprio così ...): si tratta di determinarne il periodo, con la relativa incertezza. Abbiamo a disposizione diversi metodi, ciascuno con i suoi svantaggi:

  1. Misurare gli intervalli temporali tra un picco e il consecutivo con l'aiuto del programma (Analyze/Examine), prendere nota delle misure, e calcolarne media e sigma, da assumere come indicatore di incertezza.
  2. Far eseguire il "curve fitting" al programma (Analyze/Linear Curve Fit ...), scegliendo una curva del tipo A Sin[Bx + C] + D, ottenendo i valori dei quattro parametri A, B, C, D, dei quali ci interessa B, che corrisponde ad w. Da w è facile ricavare il periodo (T=2p/w), solo che non abbiamo una procedura semplice per determinare l'incertezza;
  3. Importare il file in formato .txt in Excel, quindi (vedi file Esempio)
    1. individuare i passaggi per la posizione di equilibrio evidenziando il cambiamento di segno con una formula nella casella adiacente sulla destra (nel caso in cui il sensore non sia stato azzerato occorrerà calcolare le variazioni rispetto ad una media, determinata però non su tutti i dati, ma su un numero intero di semiperiodi)
    2. in una ulteriore colonna riportiamo solamente le variazioni dei valori della colonna precedente (ciascuno di tali valori – escluso ovviamente il primo - costituisce un semiperiodo)
    3. calcolare media e sigma dei semiperiodi e determinare i corrispondenti valori dei periodi
  4. Importare il file in formato .txt in Excel, quindi - mediante una macro - localizzare i valori massimi della forza e i tempi corrispondenti, e calcolare gli intervalli tra questi ultimi. Media e sigma di tali intervalli forniranno il periodo e la sua incertezze (si esamini la macro nel file Esempio).

La nostra serie di misure ha portato ai seguenti risultati

massa nominale
massa effettiva
massa effettiva

periodo T
sn-1(T)
e%(T)
T2
e%(T2)
e(T2)
T2/m
k
g
g
kg
s
s
s2
s2
N/m
25
25.1
0.0251
0.353
0.006
1.7%
0.12
3.4%
0.004
4.956
8.0
50
50.3
0.0503
0.468
0.004
0.9%
0.22
1.9%
0.004
4.351
9.1
75
75.5
0.0755
0.561
0.008
1.4%
0.32
2.9%
0.009
4.175
9.5
100
100.6
0.1006
0.640
0.005
0.7%
0.41
1.5%
0.006
4.067
9.7
125
125.8
0.1258
0.710
0.007
1.0%
0.50
1.9%
0.010
4.005
9.9
150
150.8
0.1508
0.773
0.009
1.2%
0.60
2.4%
0.015
3.967
10.0
175
176.1
0.1761
0.833
0.005
0.6%
0.69
1.3%
0.009
3.936
10.0
200
201.2
0.2012
0.888
0.008
0.9%
0.79
1.9%
0.015
3.919
10.1
225
226.4
0.2264
0.940
0.009
1.0%
0.88
1.9%
0.017
3.901
10.1
250
251.4
0.2514
0.988
0.005
0.5%
0.98
0.9%
0.009
3.884
10.2
275
276.8
0.2768
1.035
0.003
0.3%
1.07
0.6%
0.006
3.871
10.2
300
302
0.3020
1.079
0.011
1.0%
1.16
2.0%
0.023
3.852
10.2
325
327
0.3270
1.122
0.011
0.9%
1.26
1.9%
0.024
3.848
10.3
media
0.7
4.1
9.8
sigma
0.4
0.3
0.6

Legenda:

sn-1(T): scarto quadratico medio del periodo

e%(T): errore relativo sul periodo

e(T2) : errore assoluto sul quadrato del periodo

T2/m : rapporto tra quadrato del periodo e massa

Possiamo seguire attraverso dei grafici il significato delle colonne della tabella:

Di seguito sono rappresentati massa (in ascissa) e periodo

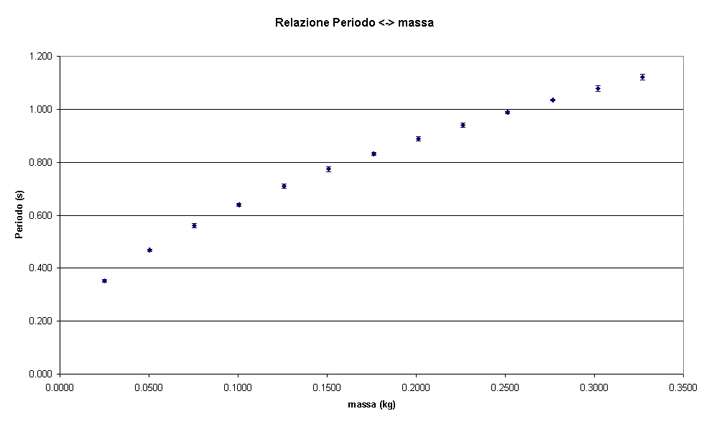
Possiamo notare che esiste una relazione apparentemente non lineare tra le due grandezze: esaminiamo ora la relazione tra massa e quadrato del periodo.

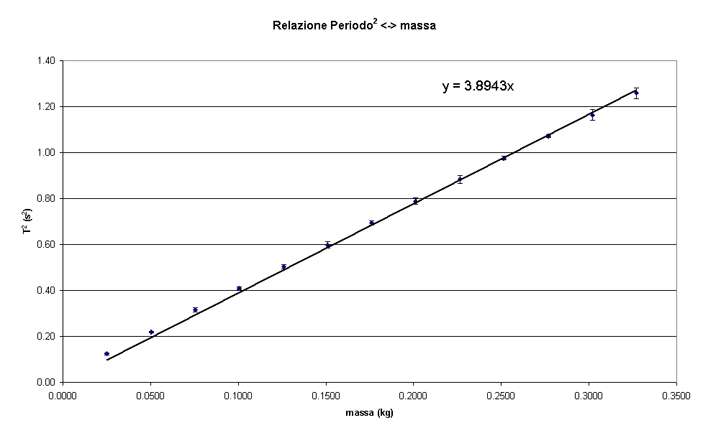
Sembrano direttamente proporzionali: una retta per l'origine è un buon modello per questa relazione, e il rapporto T2/m (vedi tabella precedente) è costante nei limiti del 7% (0.3/4.1)